IQMs for structural images
Measures based on noise measurements
cjv()– coefficient of joint variation (CJV): Thecjvof GM and WM was proposed as objective function by [Ganzetti2016] for the optimization of INU correction algorithms. Higher values are related to the presence of heavy head motion and large INU artifacts. Lower values are better.
cnr()– contrast-to-noise ratio (CNR): Thecnr[Magnota2006], is an extension of the SNR calculation to evaluate how separated the tissue distributions of GM and WM are. Higher values indicate better quality.
snr()– signal-to-noise ratio (SNR): calculated within the tissue mask.
snr_dietrich(): Dietrich’s SNR (SNRd) as proposed by [Dietrich2007], using the air background as reference.
art_qi2(): Mortamet’s quality index 2 (QI2) is a calculation of the goodness-of-fit of a \(\chi^2\) distribution on the air mask, once the artifactual intensities detected for computing the QI1 index have been removed [Mortamet2009]. Lower values are better.
Measures based on information theory
efc(): The EFC [Atkinson1997] uses the Shannon entropy of voxel intensities as an indication of ghosting and blurring induced by head motion. Lower values are better.The original equation is normalized by the maximum entropy, so that the EFC can be compared across images with different dimensions.
fber(): The FBER [Shehzad2015], defined as the mean energy of image values within the head relative to outside the head [QAP-measures]. Higher values are better.
Measures targeting specific artifacts
inu_* (nipype interface to N4ITK): summary statistics (max, min and median) of the INU field (bias field) as extracted by the N4ITK algorithm [Tustison2010]. Values closer to 1.0 are better, values further from zero indicate greater RF field inhomogeneity.
art_qi1(): Detect artifacts in the image using the method described in [Mortamet2009]. The QI1 is the proportion of voxels with intensity corrupted by artifacts normalized by the number of voxels in the background. Lower values are better.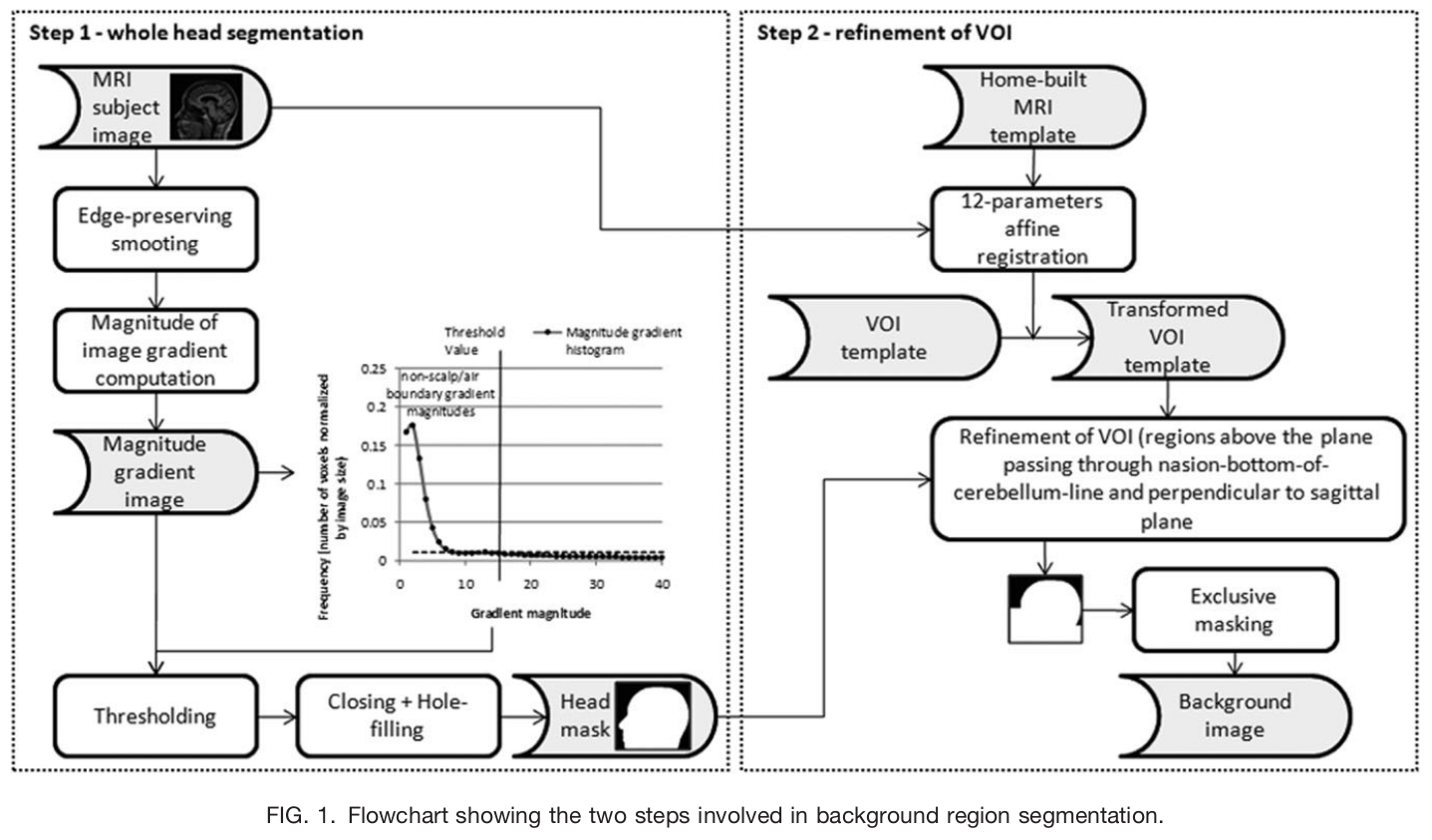
The workflow to compute the artifact detection from [Mortamet2009].
wm2max(): The white-matter to maximum intensity ratio is the median intensity within the WM mask over the 95% percentile of the full intensity distribution, that captures the existence of long tails due to hyper-intensity of the carotid vessels and fat. Values should be around the interval [0.6, 0.8].
Other measures
fwhm (nipype interface to AFNI): The FWHM of the spatial distribution of the image intensity values in units of voxels [Forman1995]. Lower values are better, higher values indicate a blurrier image. Uses the gaussian width estimator filter implemented in AFNI’s
3dFWHMx:\[\text{FWHM} = \sqrt{-{\left[4 \ln{(1-\frac{\sigma^2_{X^m_{i+1,j}-X^m_{i,j}}} {2\sigma^2_{X^m_{i,j}}}})\right]}^{-1}}\]
volume_fraction()(icvs_*): the ICV fractions of CSF, GM and WM. They should move within a normative range.
rpve()(rpve_*): the rPVe of CSF, GM and WM. Lower values are better.
summary_stats()(summary_*_*): Mean, median, median absolute deviation (mad), standard deviation, kurtosis, 5% percentile, 95% percentile and number of voxels of the distribution of background, CSF, GM and WM.
overlap_*_*: The overlap of the TPMs estimated from the image and the corresponding maps from the ICBM nonlinear-asymmetric 2009c template. Higher values are better.
\[\text{JI}^k = \frac{\sum_i \min{(\text{TPM}^k_i, \text{MNI}^k_i)}} {\sum_i \max{(\text{TPM}^k_i, \text{MNI}^k_i)}}\]
- mriqc.qc.anatomical.art_qi1(airmask, artmask)[source]
Detect artifacts in the image using the method described in [Mortamet2009]. Calculates \(\text{QI}_1\), as the proportion of voxels with intensity corrupted by artifacts normalized by the number of voxels in the “hat” mask (i.e., the background region above the nasio-occipital plane):
\[\text{QI}_1 = \frac{1}{N} \sum\limits_{x\in X_\text{art}} 1\]Near-zero values are better. If \(\text{QI}_1 = -1\), then the “hat” mask (background) was empty and the dataset is likely a skull-stripped image or has been heavily post-processed.
- Parameters:
airmask (numpy.ndarray) – input air mask, without artifacts
artmask (numpy.ndarray) – input artifacts mask
- mriqc.qc.anatomical.art_qi2(img, airmask, min_voxels=1000, max_voxels=300000, save_plot=True, coil_elements=32)[source]
Calculates \(\text{QI}_2\), based on the goodness-of-fit of a centered \(\chi^2\) distribution onto the intensity distribution of non-artifactual background (within the “hat” mask):
\[\chi^2_n = \frac{2}{(\sigma \sqrt{2})^{2n} \, (n - 1)!}x^{2n - 1}\, e^{-\frac{x}{2}}\]where \(n\) is the number of coil elements.
- Parameters:
img (numpy.ndarray) – input data
airmask (numpy.ndarray) – input air mask without artifacts
- mriqc.qc.anatomical.cjv(mu_wm, mu_gm, sigma_wm, sigma_gm)[source]
Calculate the CJV, a measure related to SNR and CNR that is presented as a proxy for the INU artifact [Ganzetti2016]. Lower is better.
\[\text{CJV} = \frac{\sigma_\text{WM} + \sigma_\text{GM}}{|\mu_\text{WM} - \mu_\text{GM}|}.\]
- mriqc.qc.anatomical.cnr(mu_wm, mu_gm, sigma_air, sigma_wm, sigma_gm)[source]
Calculate the CNR [Magnota2006]. Higher values are better.
\[\text{CNR} = \frac{|\mu_\text{GM} - \mu_\text{WM} |}{\sqrt{\sigma_B^2 + \sigma_\text{WM}^2 + \sigma_\text{GM}^2}},\]where \(\sigma_B\) is the standard deviation of the noise distribution within the air (background) mask.
- Parameters:
mu_wm (float) – mean of signal within white-matter mask.
mu_gm (float) – mean of signal within gray-matter mask.
sigma_air (float) – standard deviation of the air surrounding the head (“hat” mask).
sigma_wm (float) – standard deviation within white-matter mask.
sigma_gm (float) – standard within gray-matter mask.
- Returns:
the computed CNR
- mriqc.qc.anatomical.efc(img, framemask=None, decimals=4)[source]
Calculate the EFC [Atkinson1997]. Uses the Shannon entropy of voxel intensities as an indication of ghosting and blurring induced by head motion. A range of low values is better, with EFC = 0 for all the energy concentrated in one pixel.
\[\text{E} = - \sum_{j=1}^N \frac{x_j}{x_\text{max}} \ln \left[\frac{x_j}{x_\text{max}}\right]\]with \(x_\text{max} = \sqrt{\sum_{j=1}^N x^2_j}\).
The original equation is normalized by the maximum entropy, so that the EFC can be compared across images with different dimensions:
\[\text{EFC} = \left( \frac{N}{\sqrt{N}} \, \log{\sqrt{N}^{-1}} \right) \text{E}\]- Parameters:
img (numpy.ndarray) – input data
framemask (numpy.ndarray) – a mask of empty voxels inserted after a rotation of data
- mriqc.qc.anatomical.fber(img, headmask, rotmask=None, decimals=4)[source]
Calculate the FBER [Shehzad2015], defined as the mean energy of image values within the head relative to outside the head. Higher values are better, and an FBER=-1.0 indicates that there is no signal outside the head mask (e.g., a skull-stripped dataset).
\[\text{FBER} = \frac{E[|F|^2]}{E[|B|^2]}\]- Parameters:
img (numpy.ndarray) – input data
headmask (numpy.ndarray) – a mask of the head (including skull, skin, etc.)
rotmask (numpy.ndarray) – a mask of empty voxels inserted after a rotation of data
- mriqc.qc.anatomical.rpve(pvms, seg)[source]
Computes the rPVe of each tissue class.
\[\text{rPVE}^k = \frac{1}{N} \left[ \sum\limits_{p^k_i \in [0.5, P_{98}]} p^k_i + \sum\limits_{p^k_i \in [P_{2}, 0.5)} 1 - p^k_i \right]\]
- mriqc.qc.anatomical.snr(mu_fg, sigma_fg, n)[source]
Calculate the SNR. The estimation may be provided with only one foreground region in which the noise is computed as follows:
\[\text{SNR} = \frac{\mu_F}{\sigma_F\sqrt{n/(n-1)}},\]where \(\mu_F\) is the mean intensity of the foreground and \(\sigma_F\) is the standard deviation of the same region.
- mriqc.qc.anatomical.snr_dietrich(mu_fg, mad_air=0.0, sigma_air=1.0)[source]
Calculate the SNR.
This must be an air mask around the head, and it should not contain artifacts. The computation is done following the eq. A.12 of [Dietrich2007], which includes a correction factor in the estimation of the standard deviation of air and its Rayleigh distribution:
\[\text{SNR} = \frac{\mu_F}{\sqrt{\frac{2}{4-\pi}}\,\sigma_\text{air}}.\]
- mriqc.qc.anatomical.summary_stats(data: ndarray, pvms: dict[str, numpy.ndarray], rprec_data: int = 0, rprec_prob: int = 3, decimals: int = 4) dict[str, dict[str, float]][source]
Estimates weighted summary statistics for each tissue distribution in the data.
This function calculates the mean, median, standard deviation, kurtosis, median absolute deviation (MAD), the 95th and 5th percentiles, and the number of voxels for each tissue distribution defined by a label in the provided partial volume maps (pvms).
- Parameters:
data (
ndarray(float, 3D)) – A three-dimensional array of data from which summary statistics will be extracted.pvms (
dictofstrkeys andndarray(float, 3D) values) – A dictionary of partial volume maps where the key indicates the label of a region-of-interest (ROI) and the values are three-dimensional arrays matched in size with data and containing the probability/fraction of the voxel containing the given label.rprec_data (
int, optional (default=0)) – Number of decimal places to round the data array before calculation. Rounding alleviates floating-point error variability by explicitly rounding before quantification operations.rprec_prob (
int, optional (default=3)) – Number of decimal places to round the probability maps before calculation. Rounding alleviates floating-point error variability by explicitly rounding before quantification operations.
- Returns:
A dictionary where the keys are labels from the
pvmsdictionary and the values are dictionaries containing the following keys for each tissue distribution:- Return type: